

Sumner
The fundamental assumption of general relativity is that spacetime is curved. Accepting this, Schrödinger examined relativistic quantum mechanics with the spacetime curvature of the closed Friedmann solution to show that the wave lengths of quantum wave functions are proportional to the radius of curvature. He chose the closed solution for theoretical reasons that are confirmed by Hubble redshift measurements.Sumner studied electrodynamics with the same curved spacetime used by Schrödinger to find that the strengths of electrical fields are inversely proportional to the radius of spacetime curvature. The implications of electrical field changes are identical for photons, the energy levels of atoms, and the interpretation of redshift to those that come from Schrödinger's result.
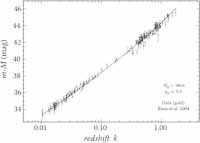
The relativistic formula relating redshift to distance is different for a contracting Friedmann universe than for an expanding one because of the signs of square roots. Sumner and Vitayaev rederived this formula, including the changes in atomic emissions as well as photon wavelengths, to find that the acceleration characteristic of contraction spectacularly agrees with the acceleration observed in modern redshift measurements.
Schrödinger and Sumner were each motivated to explore the implications of relativistic spacetime curvature on the standard physical theories of the 1930's. Those theories, general relativity, quantum mechanics, and electrodynamics, have proven to be as relevant today as they were 80 years ago.
Physicists love to use math to understand nature. If you know math, you know its intrinsic beauty. You know the rigor of its logic. You know the surprising insights it can give you. With math you can dance with the Milky Way. You can look in a mirror and see You are Star Dust. You can look in a mirror and see You are the Universe.
Bill and Dawn Sumner